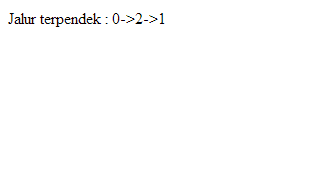Download GIS rute terpendek Algoritma Dijkstra PHP MYSQL
Download Algoritma Dijkstra PHP MySQL menggunakan framework codeigniter, tetapi maaf berdonasi. Aplikasi pencarian rute terpendek berbasis web dapat menentukan rute perjalanan dengan jarak terpendek menggunakan algoritma dijkstra.
Pengenalan Algoritma Dijkstra
Algoritma Dijkstra dinamai menurut penemunya, seorang ilmuwan komputer Edsger Dijkstra, adalah sebuah algoritme rakus (greedy algorithm) yang dipakai dalam memecahkan permasalahan jarak terpendek (shortest path problem) untuk sebuah graf berarah (directed graph) dengan bobot-bobot garis (edge weights) yang bernilai nonnegatif, { [0,infty ). Input algoritma ini adalah sebuah graf berarah yang berbobot (weighted directed graph) 
Misalnya, bila titik dari sebuah graf melambangkan kota-kota dan bobot garis melambangkan jarak antara kota-kota tersebut, algoritme Dijkstra dapat digunakan untuk menemukan jarak terpendek antara dua kota.
Biaya (cost) dari sebuah garis dapat dianggap sebagai jarak antara dua simpul, yaitu jumlah jarak semua garis dalam jalur tersebut. Untuk sepasang titik s dan t dalam V, algoritma ini menghitung jarak terpendek dari s ke t.

Landasan Teori Download Algoritma Dijkstra
Algoritma Dijkstra bekerja dengan membuat jalur ke satu simpul optimal pada setiap langkah. Jadi pada langkah ke n, setidaknya ada n node yang sudah kita tahu jalur terpendek. Langkah-langkah algoritma Dijkstra dapat dilakukan dengan langkah-langkah berikut:
- Tentukan titik mana yang akan menjadi node awal, lalu beri bobot jarak pada node pertama ke node terdekat satu per satu, Dijkstra akan melakukan pengembangan pencarian dari satu titik ke titik lain dan ke titik selanjutnya tahap demi tahap.
- Beri nilai bobot (jarak) untuk setiap titik ke titik lainnya, lalu set nilai 0 pada node awal dan nilai tak hingga terhadap node lain (belum terisi) 2.
- Set semua node yang belum dilalui dan set node awal sebagai “Node keberangkatan”
- Dari node keberangkatan, pertimbangkan node tetangga yang belum dilalui dan hitung jaraknya dari titik keberangkatan. Jika jarak ini lebih kecil dari jarak sebelumnya (yang telah terekam sebelumnya) hapus data lama, simpan ulang data jarak dengan jarak yang baru
- Saat kita selesai mempertimbangkan setiap jarak terhadap node tetangga, tandai node yang telah dilalui sebagai “Node dilewati”. Node yang dilewati tidak akan pernah di cek kembali, jarak yang disimpan adalah jarak terakhir dan yang paling minimal bobotnya.
- Set “Node belum dilewati” dengan jarak terkecil (dari node keberangkatan) sebagai “Node Keberangkatan” selanjutnya dan ulangi langkah e.
Sebagai contoh hitunglah Jarak terdekat dari V1 ke V7 pada gambar berikut ini.
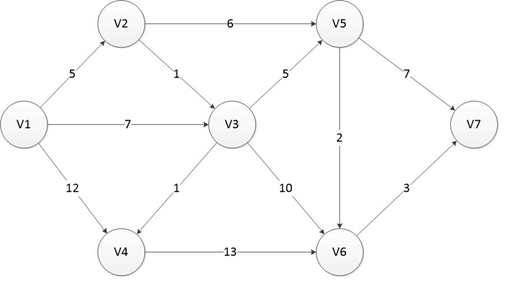
Hasil setiap stepnya dapat dilihat pada tabel berikut ini.
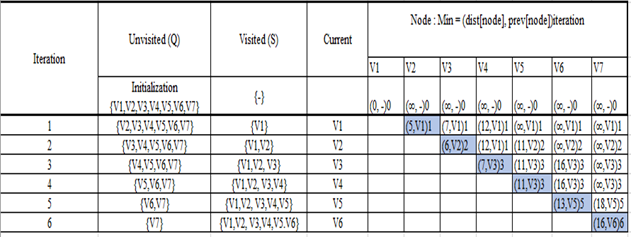
Dengan demikian jarak terpendek dari V1 ke V7 adalah 16 dengan jalur V1->V2->V3->V5->V6->V7
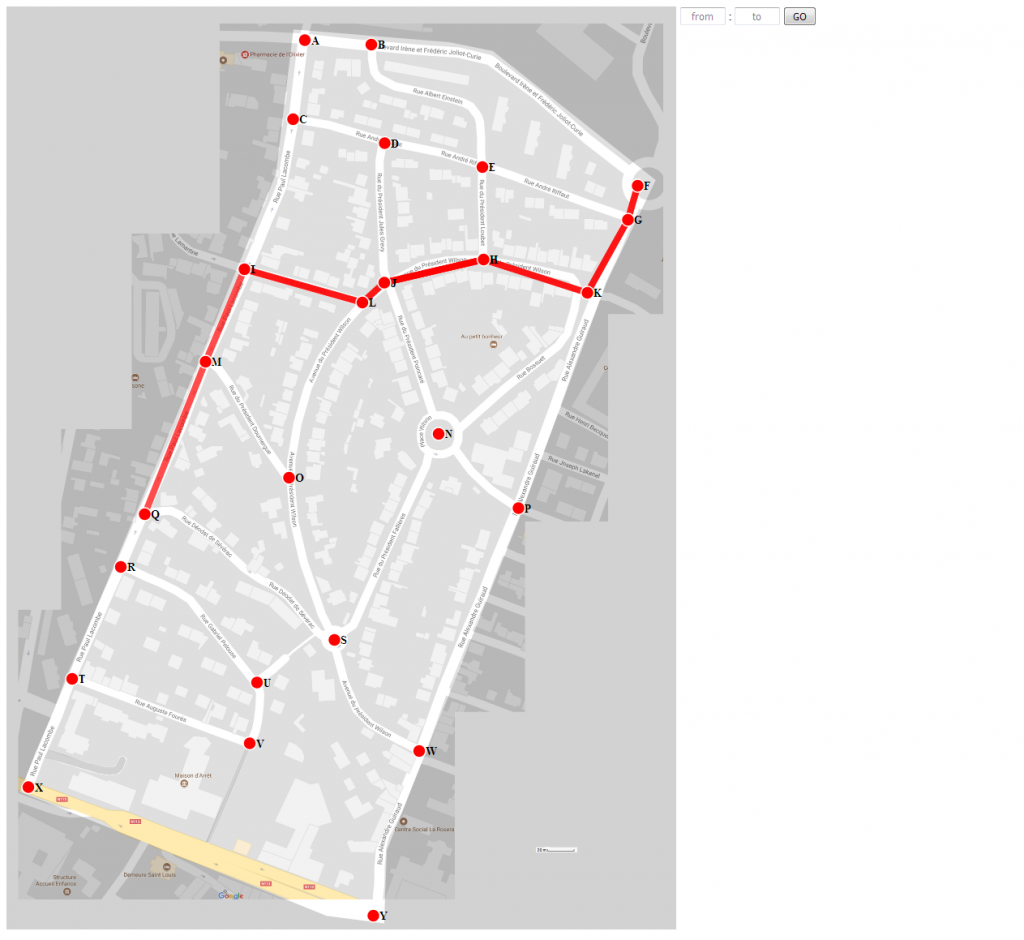
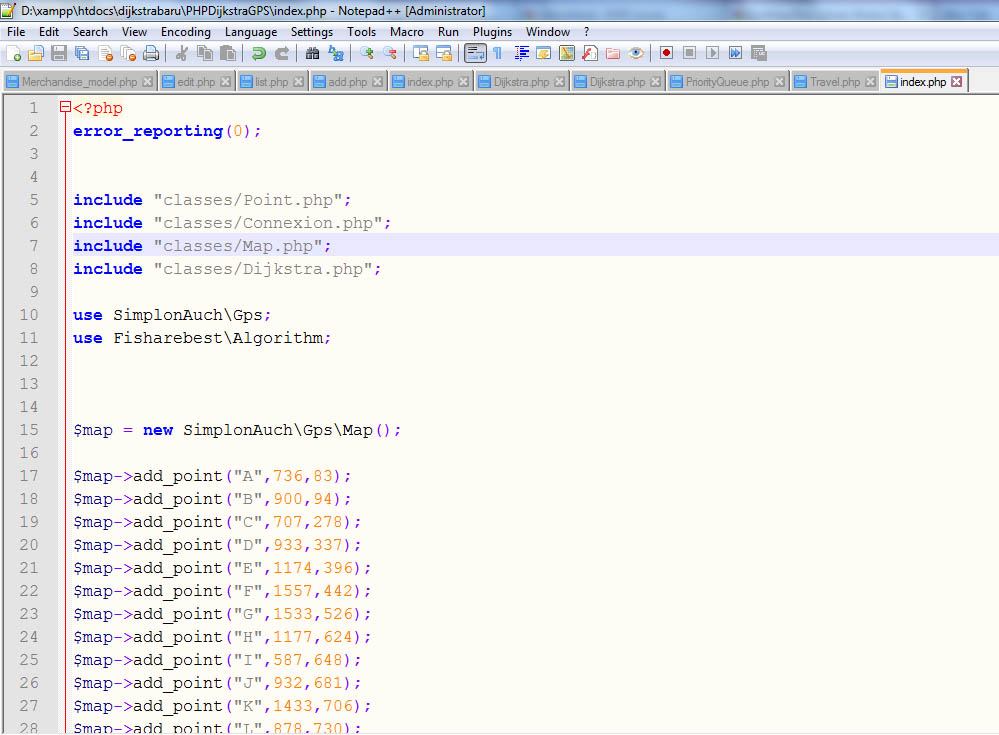
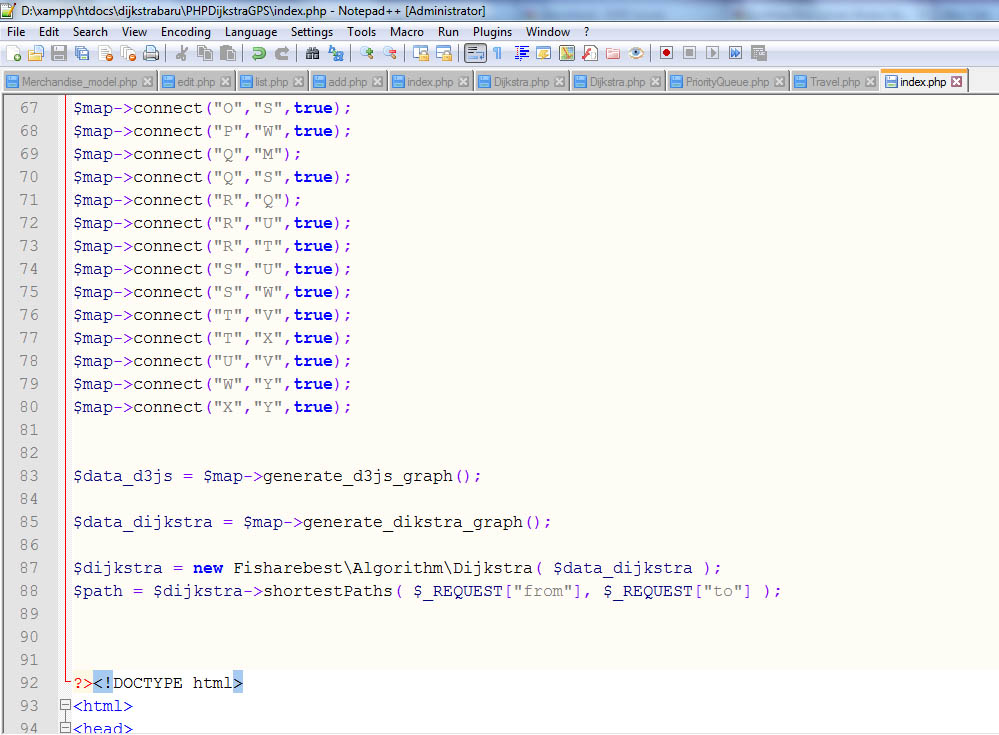
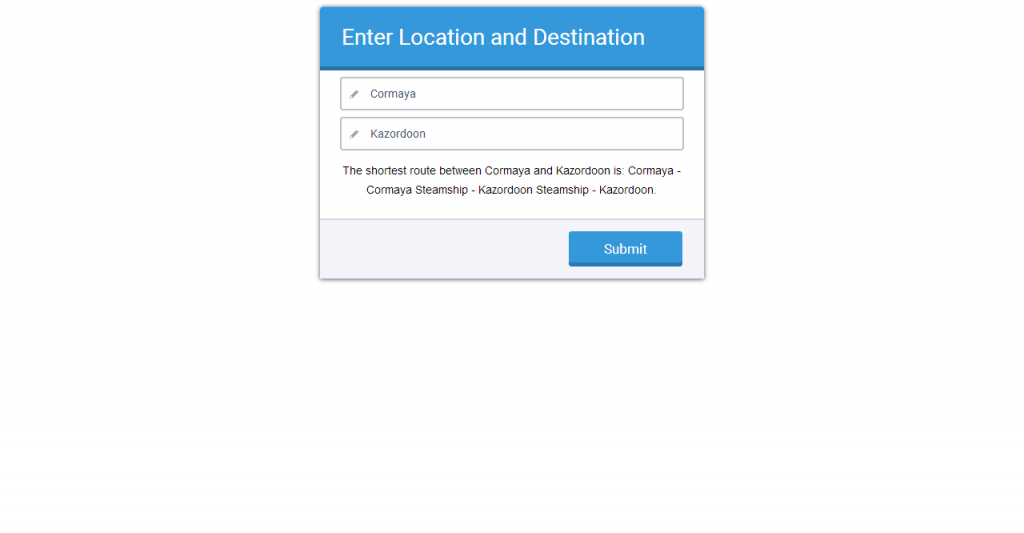
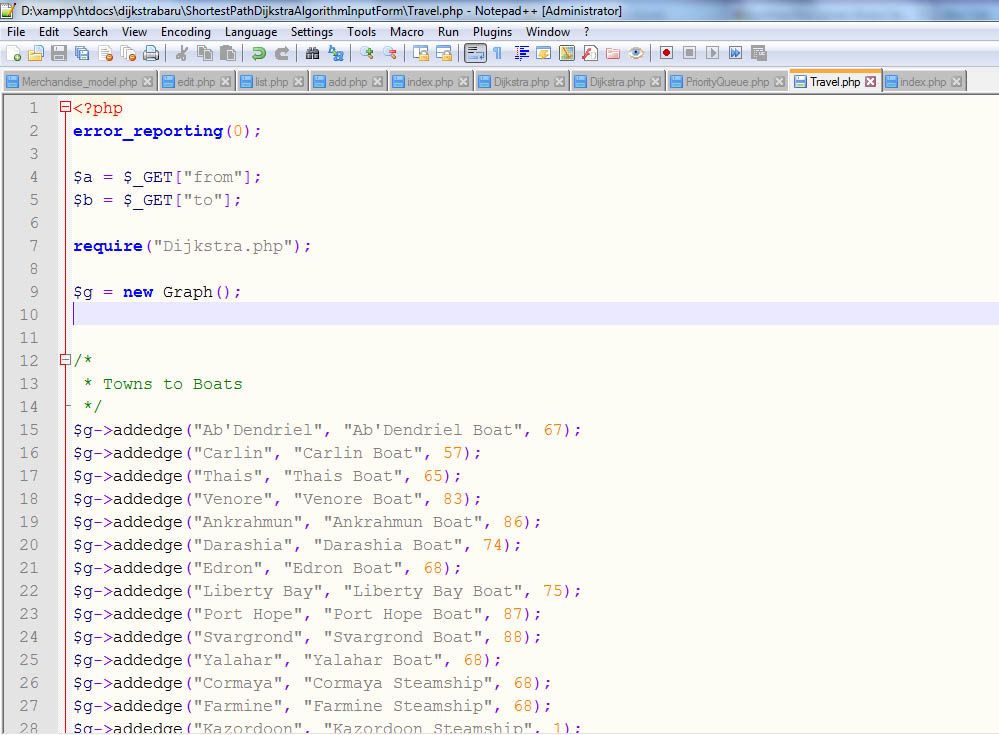
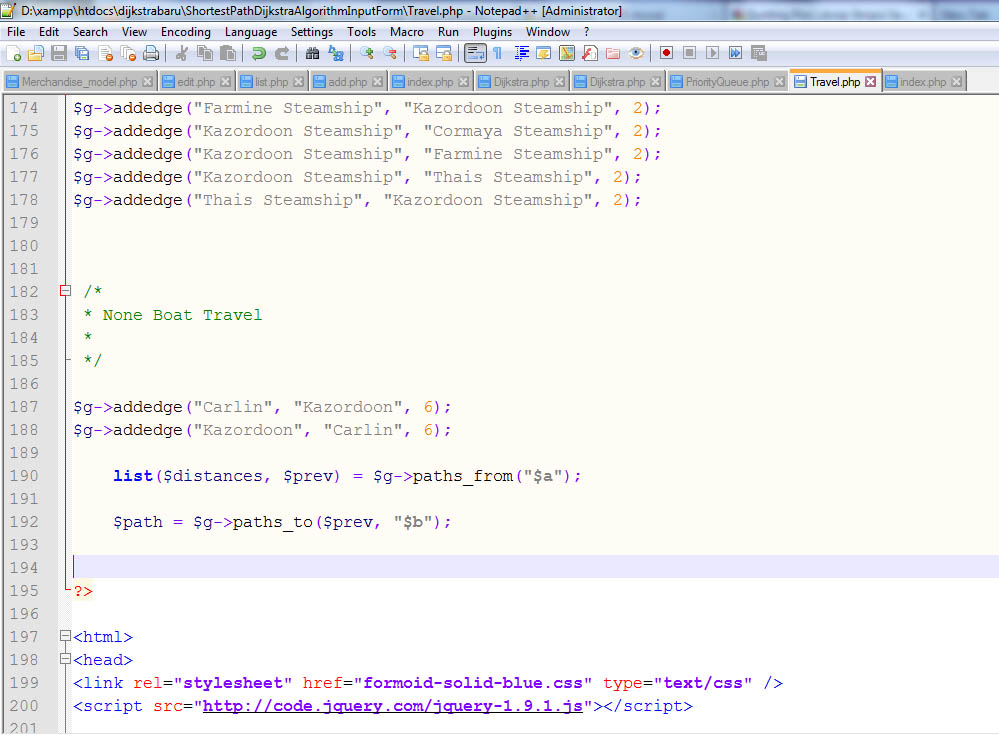
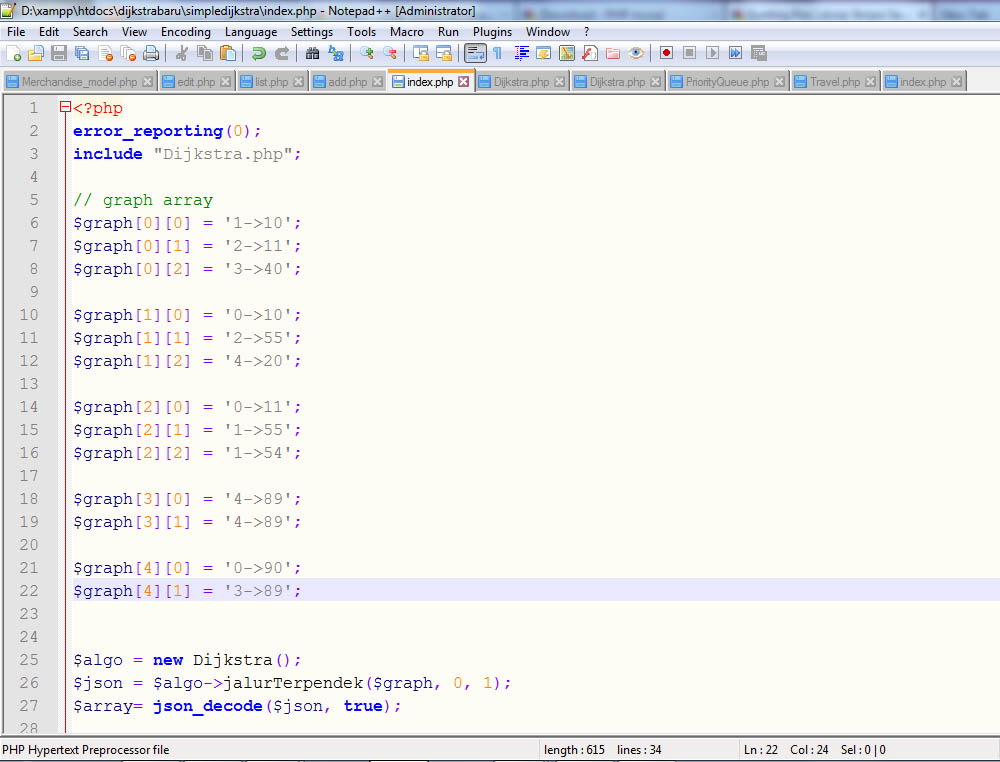
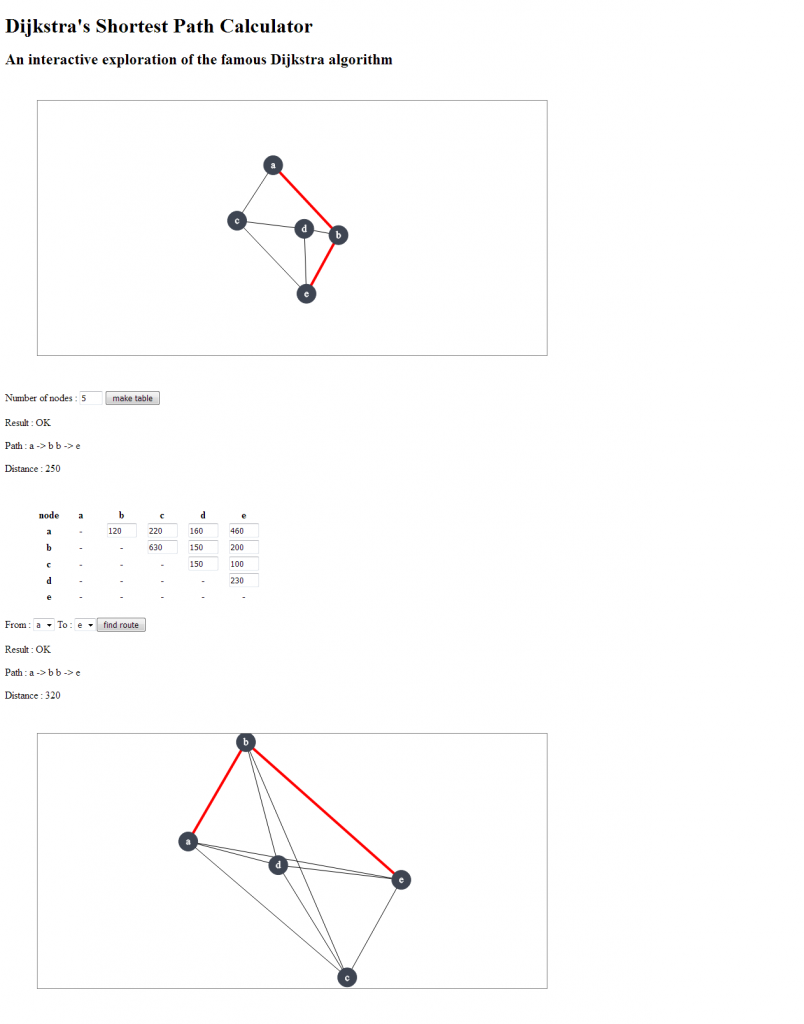
Screenshot Aplikasi Dijkstra
sdsadsa
Mesin Dijkstra
Mesin Dijkstra Lainnya